Wear Equations

Wear Equations

As discussed earlier, estimating the service life of Power Screw systems is a very complex task and inexact at best. The only reliable predictor is actual testing. Variations in service life are widely scattered and multiples of two to one or three to one in life test performance are not uncommon. The field of tribology is not as yet mature enough for accurate life estimating. The variables affecting life are too great in number and can vary too widely preventing reliable performance predictions. To illustrate the complexity of predicting wear theoretically, consider the potential equation for predicting wear in Figure 40.

The exponents x thru j may be unity or greater than or less than unity and much work remains to be done by tribologists to determine a workable formula which includes all variables known to influence wear. In the meantime, the assumption commonly used for power screw and nut wear is that within the mating materials’ PV limits, wear is proportional to the operating PV. This is known as the “linear assumption of wear” and while not completely true it is a useful estimator.

Using the linear assumption and with reference to Figure 41, two mating materials are assumed to have a “PV LIMIT” which is constant except for the extremes of unit pressure and surface speed. This relationship is represented by the graph in Figure 41. Below the PV limit curve, the linear wear life assumption states that wear is proportional to the PV product. Thus, simplifying Equation 1 in Figure 40, x and y both become unity and all the variables beyond V are eliminated. This yields the following linear equation for wear life:

Wear = KPV Equation 2

In English units of measure for the above equation, Wear is the rate of wear in inch/hr, K is the “wear factor” in in.3-min./ ft.-lb.-hr., P is the pressure in lbs./in2 (PSI),V is the rubbing surface speed in ft./min. (FPM). Note that Wear from this equation is the slope of the linear section of the graph in Figure 37.

Example Using Equation 2

Equation 2 may be more useful in relative application than in the absolute application because “K” factors for common lubricated bronzes and lubricated plastics are not plentiful.

Let €(tm)s assume however that testing of a 3/4 – 6 ACME screw with lubricated bronze sleeve nut yields a service life of 20,000 cycles for a 10-inch travel at 1,000 lbs. and 300 RPM. The target service life is 30,000 cycles.

• We could calculate the “K” factor from this test result, but that is not necessary to evaluate the expected increase in service life by changing to a larger 1 – 5 ACME size with lubricated bronze sleeve nut.
• For the 3/4 – 6 size, the speed V at 300 RPM is 59 FPM and using the thread contact area of 1.414 sq. inches, the pressure P is 707 PSI at 1,000 lbs. load.
• This yields an operating PV of 41,713 PSIFPM.
• For the larger ACME size 1 – 5 note that the speed can be reduced to 250 RPM to get the same linear speed for the end-use because the lead is .200 in./rev. versus .16667 in./rev. for the 3/4 – 6 size.
• Using the same load of 1,000 lbs. but the larger contact area of 2.55 sq. inches, the pressure P becomes 392 PSI and the speed V at 250 RPM is now 65.6 FPM reducing the operating PV to 25,715 PSIFPM.
• The theoretically expected life would then increase by 62% (41,713 / 25,715 = 1.62) to 32,400 and the target service life would be achieved.

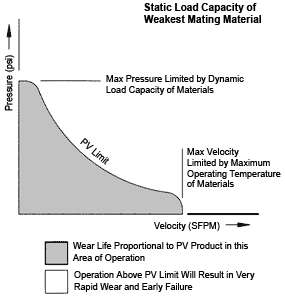
FIGURE 41

Cost Considerations

The products in this catalog are arranged in increasing cost order from front to back. ACME’s are the least expensive and are the most widely used. Hileads®, Torqsplines®, and Ball Screws offer increased performance at increased costs.

The final choice depends upon the user’s economics, the market for the end product, reliability objectives, and many other factors.

• Bear in mind that the initial cost is only one element in the cost equation.
• Installed cost, maintenance, consequences of failure and many other items need to be weighed before finalizing any design.