The primary concern in any screw and nut system is the amount of load to be moved. The load must be determined by the designer before the proper type and size of screw can be selected. If the load is to be moved vertically, the nut load is equal to the weight to be moved plus the friction load. If a load is to be moved horizontally, the weight must be multiplied by the coefficient of friction to determine the net load on the nut. Loads can also be measured with a spring scale or dynamometer.
Load Basics
For loads that are neither horizontal or vertical, this may be the easiest method. (Refer to Table 39 for Typical Coefficients of Friction.) The higher the load, the larger the size of the screw and nut that will be needed. Using the Screw/Nut Engineering Data provided for each screw series, select a size with static and operating load ratings as large or larger than the application loading.
Types of Loading
Tension loading is always preferred in any screw and nut system. In compression loading, screws may fail by elastic instability (buckling) and safe column loading must be investigated. (See Column Loading and Torsional & Axial Deflection sections for more comments on the effects of load on screw and nut systems.)
All screw and nut systems perform best when loaded on their axes. This is called axial loading because the screw and nut are loaded in line with the central axis. Radial (side) loading and off center (moment) loads are detrimental and should be avoided or minimized.
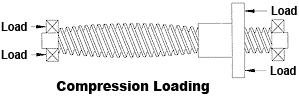
FIGURE 21
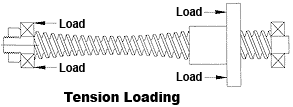
FIGURE 22
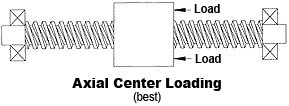
FIGURE 23
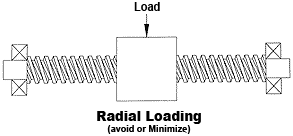
FIGURE 24
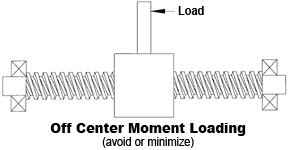
FIGURE 25
Drive Torque
Using the drive torque ratios from the Screw/Nut Engineering Data for the selected screw series, the torque can be easily calculated. The drive torque is equal to the load (lbs.) times the drive torque ratio (in.-lbs./lbs.). For example, the torque required to drive 1,000 lbs. using a 1 – 5 size Acme screw is 102 in. – lbs. (1,000 lbs. x .102 in. – lbs./lbs. = 102 in.-lbs.). The drive torque ratios listed are for the screw and nut only.
Support bearings and other drive components will require additional torque. Also, additional torque may be needed for acceleration and to overcome starting friction in the drive system which is often higher than running friction. When sizing motors and other drive components, this additional torque should be included.